Deep learning models have proven to be incredibly powerful in the field of machine learning. However, one of their limitations is the requirement for large amounts of data to train effectively. Additionally, the complexity of these models makes it challenging to interpret their understanding of the data. In such cases, linear models can be a valuable alternative. Linear regression and logistic regression are linear models that can help overcome these challenges, especially when dealing with linearly separable data.
In Edge Impulse we provide support for linear models in several ways. Firstly, you can use Keras with a single dense layer with a single neuron for linear regression or multiple neurons corresponding to the number of classes in your data for logistic regression. Secondly, you can train a scikit-learn model and encapsulate it into a custom block which can then be converted into Tensorflow Lite.
Using Keras is straightforward as you can implement the model architecture in Edge Impulse studio GUI. However, when working with limited amounts of data, it becomes crucial to carefully tune the number of epochs and the learning rate to achieve optimal results. On the other hand, the scikit-learn approach requires a few additional steps in setting up the custom block in your Edge Impulse account but has the added benefit of using scikit-learn’s battle-tested optimization techniques that will likely yield a suitable model with less hyperparameter tuning.
The most significant advantage of utilizing linear models is the direct mapping between each weight in the model and one of the input features. This property allows you to gain a deep understanding of how each feature influences the model’s predictions. Consequently, this insight can be invaluable for solving business problems or reducing the feature set used for modeling.
Below are some examples of linear models available in the scikit-learn package.
Linear regression
Linear regression aims to find the best-fitting line that represents the linear association between the variables. This line can then be used to predict a scalar-dependent variable.
Logistic regression (LogisticRegression and LogisticRegressionCV)
Logistic regression is an extension of linear regression, specifically designed for classification problems. The model learns to predict the probability of input features belonging to a certain class.
Ridge regression (Ridge and RidgeCV)
Ridge regression is a variation of linear regression that incorporates a technique called L2 regularization, which penalizes unimportant features to enhance the model’s performance. The level of penalization can be controlled.
Ridge classification (RidgeClassifier and RidgeClassifierCV)
Ridge classification is logistic regression but with L2 regularization. This version of the algorithm is used for classification rather than prediction of a singular value.
Keep in mind that it’s essential to exercise caution when working with linear models. These models are sensitive to the values of features, so it is recommended to ensure that the features are of the same magnitude. If the features have different scales, it is advisable to standardize them before training a linear model.
By leveraging linear models, you can accomplish more even with limited amounts of data. Their interpretability and feature mapping provide valuable insights and a practical means of tackling various machine-learning challenges.
How can you use these models in Edge Impulse?
Scikit learn implementations of the models outlined above can be added to your personal account or organization as custom ML blocks by following the instructions in the github repo here: https://github.com/edgeimpulse/sklearn-linear-models
These blocks have been configured to show the most common hyperparameters in the Edge Impulse studio GUI but if you wish to access more you can edit the train.py and parameters.json files to access any of scikit learn’s hyperparameters.
For enterprise users: you can also use these custom blocks within the EON tuner. Including the powerful option to specify custom hyperparameters to the custom blocks and allowing EON tuner to find the best hyperparameters for your project.
Example
Temperature regression tutorial data from here: https://studio.edgeimpulse.com/public/17972/latest
Trained with Edge impulse default 2 dense layers NN (20 and 10 neurons):
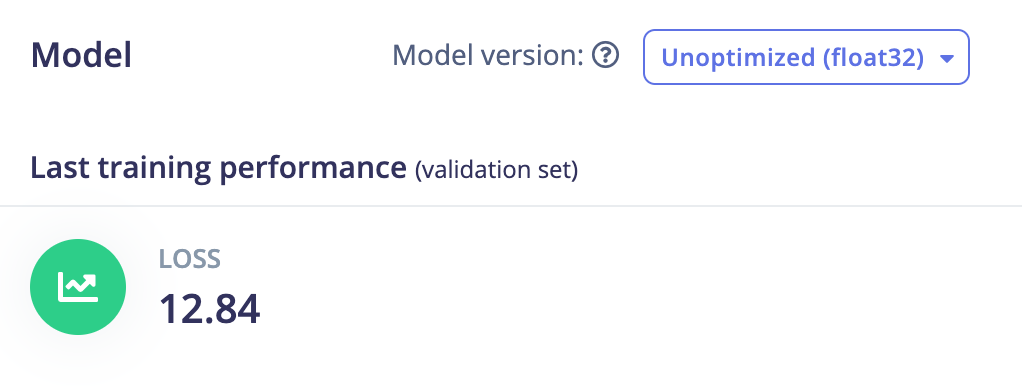
Keras single neuron dense layer:
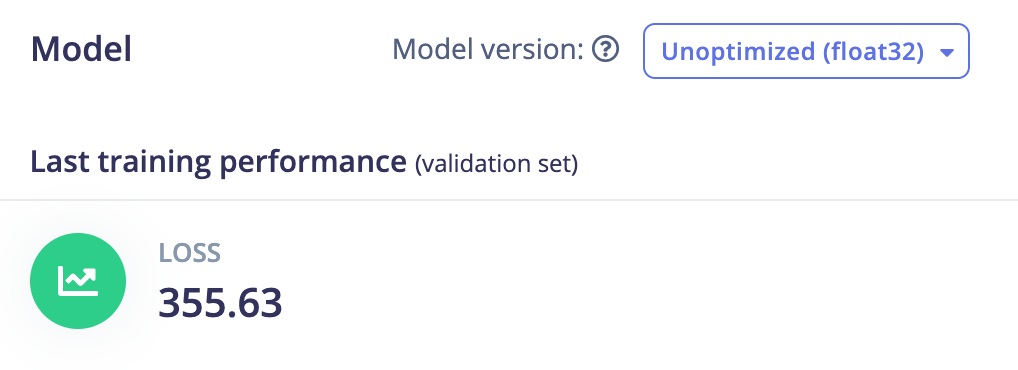
Scikit learn LinearRegression:
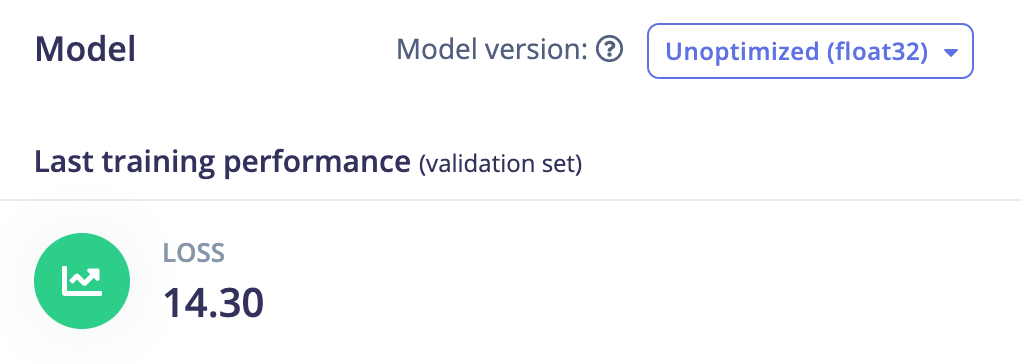
Scikit learn Ridge:
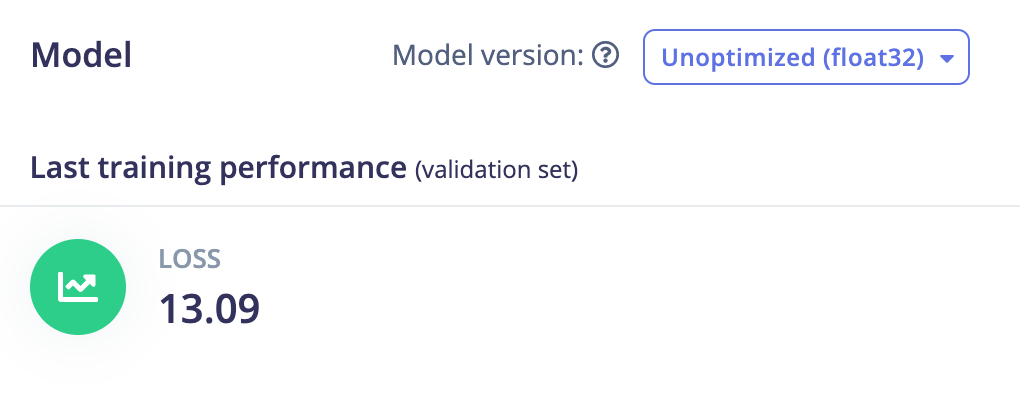
Scikit learn RidgeCV:
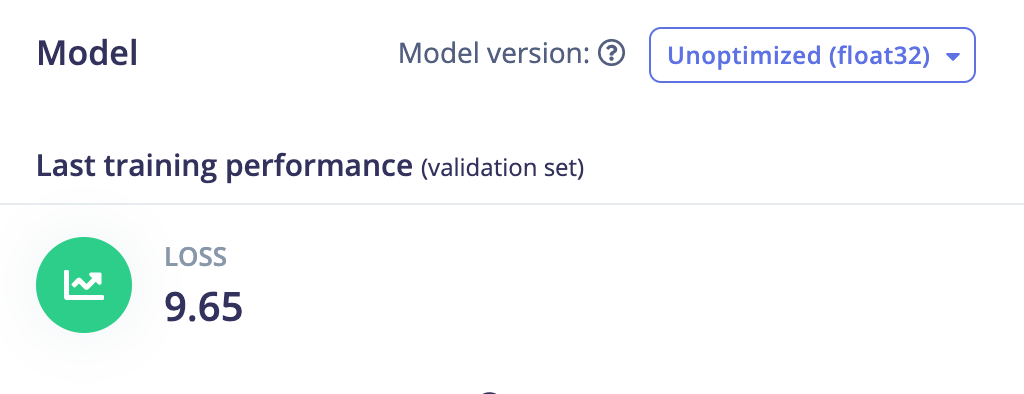
The CV version of Ridge uses cross-validation to test several values for the hyperparameter of Ridge which is called alpha and then select the best-performing one.
You can download one of the trained models from the project dashboard and load them into Netron to see the weights of the model:
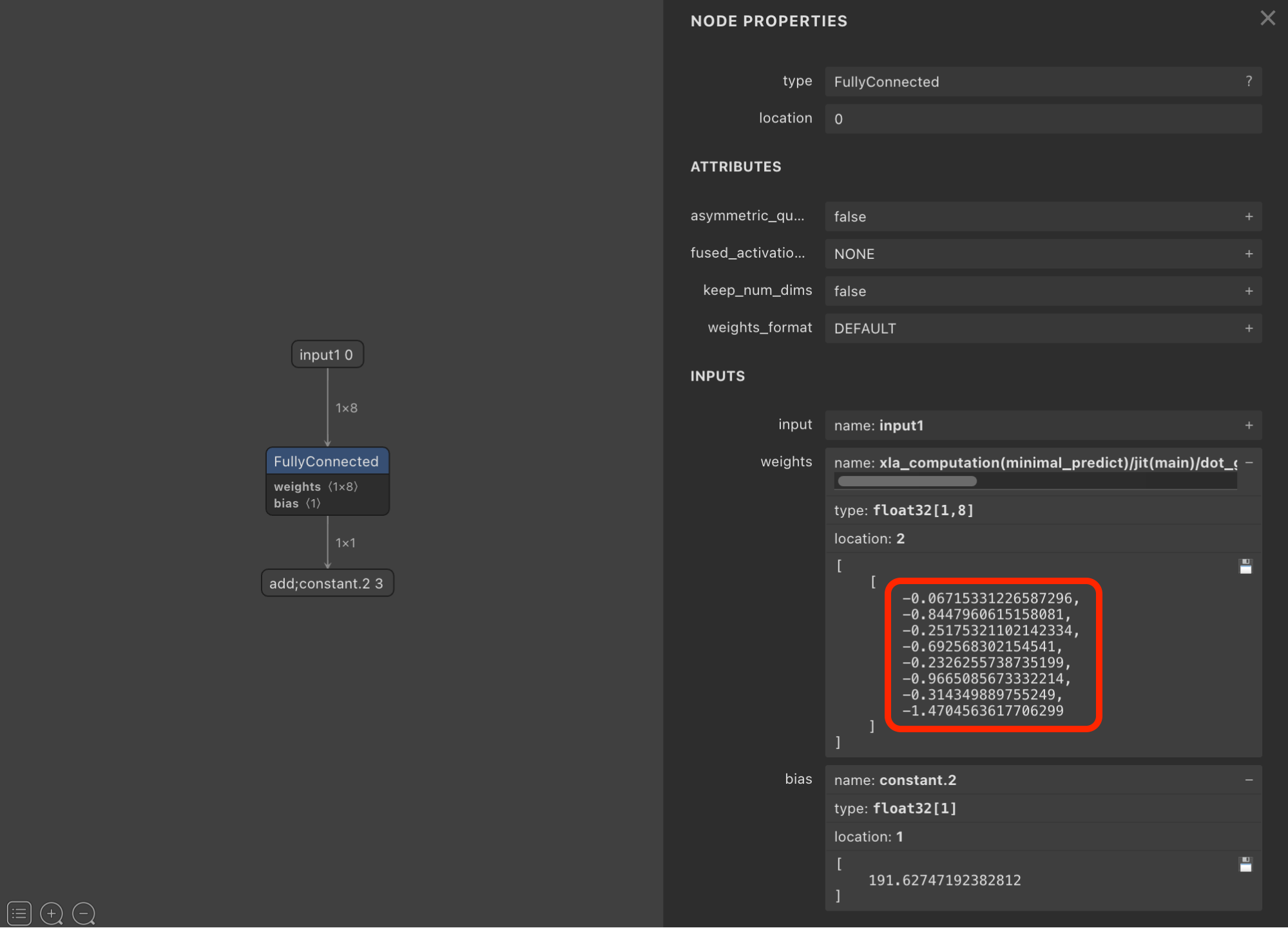
The weights in this model (8 values in the red box) tell us that the 8th feature in our data has the largest impact on the model because this feature has the largest absolute value. In this example, the input features are from a temperature sensor but this interpretability can be used with any model input features.
For classification models, the weights are a matrix where the number of rows equals the number of input features and the number of columns equals the number of classes.
In conclusion, Sklearn linear models offer a valuable alternative to deep learning models when faced with limited data and the need for interpretability. Their direct mapping between weights and input features provides insights that can aid in solving business problems and reducing the feature set. If you have any questions or need assistance, our documentation provides detailed information on how to set up a custom learning block. Also, our developer relations team and our community are always ready to support and collaborate with you on your machine-learning journey through our forum.
